隐含波动率(Implied Volatility, IV)是金融市场中一个重要的概念,尤其在期权交易中扮演着关键角色。它是指市场对某一资产未来波动性的预期,通常通过期权的市场价格反推而得。隐含波动率不仅影响期权的定价,还可以反映市场情绪和风险偏好,理解隐含波动率的计算公式和其背后的逻辑,对于投资者来说至关重要。
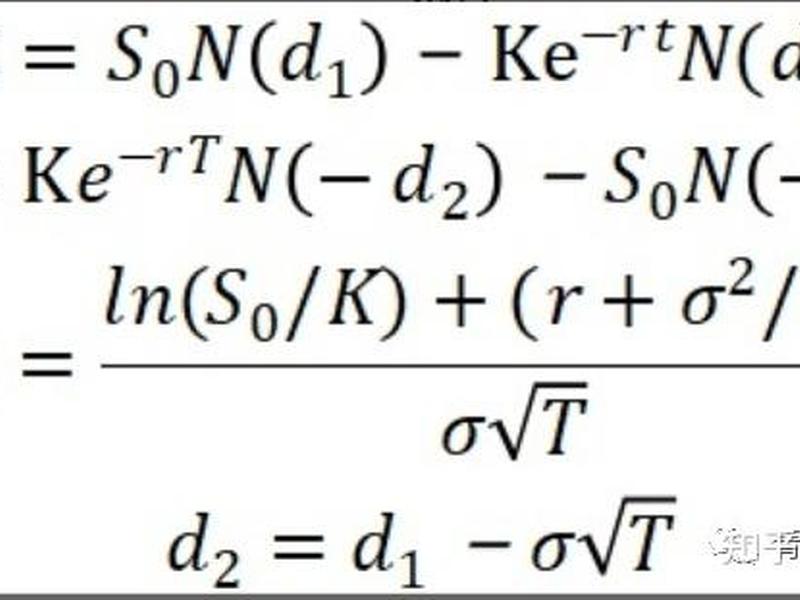
隐含波动率的基本概念
隐含波动率是投资者对标的资产未来价格波动的预期,通过期权市场上的期权价格来反映。它与历史波动率和实现波动率不同,后者分别反映过去的价格波动和实际发生的价格变化。高隐含波动率意味着市场预期价格将大幅波动,因此期权价格较高;反之,低隐含波动率则表示市场预期价格稳定,期权价格较低。
隐含波动率的计算通常依赖于Black-Scholes模型,这是一个广泛使用的期权定价模型。通过输入已知参数,如标的资产当前价格、行权价、无风险利率、到期时间等,可以得到一个合理的隐含波动率。由于隐含波动率本身是未知量,因此计算过程通常需要迭代 xxx 来求解,使得模型价格与市场实际价格相符。
隐含波动率的计算公式
隐含波动率的计算公式基于Black-Scholes模型,其原始公式为:
C=S⋅N(D1)−L⋅e−γT⋅N(D2)C=S\cdot N(D_1)-L\cdot e^{-\gamma T}\cdot N(D_2)C=S⋅N(D1)−L⋅e−γT⋅N(D2)
其中:
CCC 是看涨期权的价格
SSS 是标的资产当前价格
LLL 是行权价
γ\gamma γ 是无风险利率
TTT 是到期时间
N(D1)N(D_1)N(D1) 和 N(D2)N(D_2)N(D2) 是标准正态分布函数
D1D_1D1 和 D2D_2D2 的计算公式为:
D1=ln(S/L)+(γ+σ2/2)TσTD_1=\frac{\ln(S/L)+(\gamma +\sigma^2/2)T}{\sigma \sqrt{T}}D1=σT在这些公式中,唯一未知的变量是隐含波动率(σ\sigma σ),通过输入其他已知参数,可以反推得到隐含波动率。
影响隐含波动率的因素
隐含波动率受到多种因素的影响,其中包括市场情绪、宏观经济数据、公司财报等。当市场对某一资产未来的不确定性增加时,隐含波动率往往会上升。例如,在公司发布财报前,投资者通常会预期可能出现较大价格变动,因此隐含波动率会显著上升。地缘政治事件或经济政策变化也可能导致市场情绪剧烈变化,从而影响隐含波动率。
供求关系也是影响隐含波动率的重要因素。当某个期权受到强烈需求时,其价格会上涨,从而导致隐含波动率上升;相反,如果供给过剩,则可能导致隐含波动率下降。这种供需关系不仅体现在单一资产上,也可以在整个市场中观察到。
历史与实现波动率比较
历史波动率是基于过去实际价格数据计算得出的,它提供了对资产过去表现的一种量化评估。而实现波动率则是指在特定时间段内实际发生的价格变化。相比之下,隐含波动率则是对未来不确定性的预测,它能够更好地反映市场参与者对未来风险的看法。投资者在制定交易策略时,可以将这三种不同类型的波动率结合起来进行分析,以便更准确地判断市场趋势。
通过比较历史和隐含波动率,投资者可以识别出潜在的交易机会。当历史波动率高于隐含波动率时,可能表明市场对未来风险低估,此时可能适合做多;反之亦然。
相关内容的知识扩展:
在深入了解隐含波动率后,我们可以从多个方面进行知识扩展,以增强对这一概念的理解和应用。
之一方面:套利策略
投资者可以利用隐含波动率进行套利。例如,通过分析不同资产或同一资产不同到期日间的隐含波动率差异,投资者可以发现潜在的不合理定价,从而进行买入或卖出操作,以获取利润。在市场情绪极度乐观或悲观时,利用高低不同的隐含波动率进行对冲也是一种有效策略。
第二方面:风险管理
了解并监测隐含波动率对于风险管理至关重要。投资者可以根据隐含波动率变化调整其投资组合,以降低潜在损失。例如,当隐含波动率上升时,意味着市场不确定性增加,此时投资者可能会选择减仓或采取保护性措施,以应对可能出现的大幅度价格变动。
第三方面:技术分析工具
许多交易平台提供基于隐含波动率的数据分析工具,这些工具可以帮助投资者更直观地理解市场情绪和潜在风险。例如,通过绘制隐含波动率曲线图,可以观察到不同到期日和行权价下的隐含波动情况,从而帮助投资者制定更为精准的交易决策。这些工具也能与其他技术指标结合使用,提高交易策略的有效性。
通过上述扩展,我们不仅加深了对隐含波动率计算公式及其应用场景的理解,也为实际交易提供了更为全面和系统化的 xxx 论。













